Descrizione del meccanismo
La leva è una macchina semplice costituita da un fulcro e da due bracci che collegano il fulcro ai corpi (uno resistente e uno agente) da sollevare. Una leva è in equilibrio quando i momenti dei due bracci si equivalgono (P x D = p x d). In una leva in equilibrio è possibile individuare il centro di gravità del sistema leva, ovvero quel punto intorno al quale coesistono parti di uguali momenti (a).
In base al rapporto tra forza resistente e forza applicata, esistono diverse tipologie di leva: svantaggiosa (per mantenere uno stato di equilibrio la forza applicata è maggiore della forza resistente), vantaggiosa (per mantenere uno stato di equilibrio la forza applicata è inferiore alla forza resistente), indifferente (per mantenere uno stato di equilibrio la forza applicata è equivalente alla forza resistente). In base alla posizione del fulcro, la leva può essere di primo genere (il fulcro è posto tra la forza resistente e la forza applicata), di secondo genere (la forza resistente è tra la forza applicata e il fulcro) e di terzo genere (la forza applicata è tra la forza resistente e il fulcro).
Fin dall’antichità si aveva esperienza del fatto che corpi pesanti potessero essere più facilmente sollevati utilizzando stanghe sufficientemente lunghe. Infatti, nei cantieri spesso si usavano lunghe leve per sollevare massi pesanti. Vitruvio nel De Architectura, Libro X, Capitolo VIII, spiega le modalità d’impiego della leva nei cantieri e in ambito nautico. Si può ridurre al principio della leva, scrive ancora Vitruvio, la distribuzione di peso sulle spalle dei facchini o sugli animali uniti dal giogo.
E’ possibile individuare una prima riflessione sul principio della leva nella Questione III dei Questioni Meccaniche attribuite ad Aristotele. Secondo l’autore il braccio della leva può essere equiparato al raggio di un cerchio. A parità di forza applicata, più il raggio è lungo (e quindi il braccio) più si ottiene un maggiore spostamento. La maggiore facilità di movimento del braccio più lungo deriva dal fatto che il braccio più lungo è equiparato dall’autore a un raggio di un cerchio maggiore, mentre il braccio più corto a un raggio di un cerchio minore. Nella Questione I l’autore spiega che se prendiamo in considerazione due cerchi concentrici (DBCE e NMPO), e quindi uno con raggio maggiore (AB) e uno con raggio minore (AM), allora in tempi uguali due punti (B e M) di ciascun cerchio, posti sulla stessa perpendicolare verticale passante per il centro (BE), copriranno una porzione di circonferenza con lunghezza diversa (rispettivamente BSF e MHL). In una stessa unità di tempo, il punto (B) del cerchio più grande (DBCE) coprirà un tratto maggiore di circonferenza (BSF) rispetto al punto (M) del cerchio più piccolo (MHL). Pertanto, più lungo è il braccio, maggiore è la sua velocità di movimento (b). Secondo Aristotele a questa spiegazione può essere ricondotto il principio della leva: se due corpi equipesanti sono posti su una leva avente bracci a diversa distanza dal fulcro, il corpo più distante dal fulcro si muoverà più velocemente dell’altro.
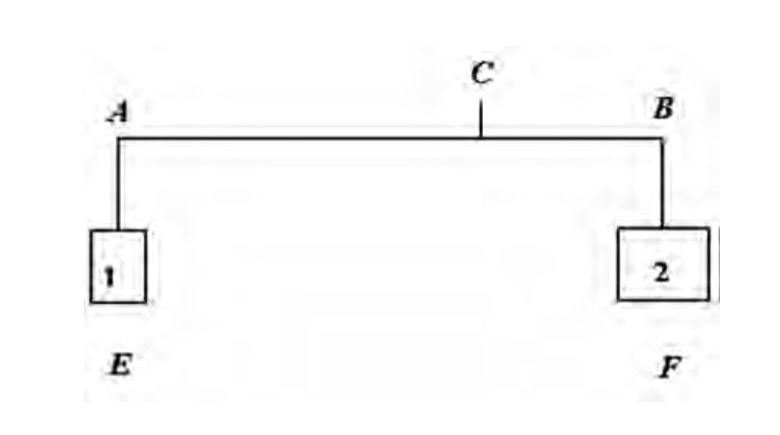
Possiamo trovare una prima trattazione geometrica del principio della leva nella Proposizione 6 del primo libro Sull’equilibrio dei piani di Archimede (a). Essa si basa sull’idea che ci sia una relazione tra i pesi (E e F) posti su una leva e le rispettive distanze dal fulcro (AC e CB). In altri termini, che sussista il seguente rapporto di proporzionalità inversa E : AC = F : CB.
La Proposizione 6 dimostra che Le grandezze commensurabili sono in equilibrio se sospese a distanze inversamente proporzionali ai pesi. Tale proposizione si basa su sette postulati:
Postulati.
I . Postuliamo che pesi uguali a uguali distanze sono in equilibrio, e che pesi uguali a distanze diseguali non sono in equilibrio, ma pendono verso il peso che è a distanza maggiore.
II. Che se, quando pesi a determinate distanze sono in equilibrio, qualcosa viene aggiunto ad un solo peso, essi non sono più in equilibrio, ma pendono verso quel peso a cui è stato aggiunto qualcosa.
III . Che, similmente, se qualcosa viene tolto da uno solo dei due pesi, essi non sono più in equilibrio, ma pendono verso quel peso da cui non è stato tolto niente.
IV. Che quando figure uguali e simili vengono fatte coincidere, i loro centri di gravità parimenti coincidono.
V. Che in figure che sono diseguali, ma simili, i centri di gravità saranno similmente situati.
VI . Che se grandezze a determinate distanze sono in equilibrio, anche altre [grandezze] uguali ad esse saranno in equilibrio alle stesse distanze.
VII . Che in ogni figura il cui perimetro è concavo nella stessa direzione il centro di gravità deve essere interno alla figura.
Per comprendere la Proposizione 6 è necessario spiegare brevemente il significato del postulato I, del postulato VI, della Proposizione 5 (Se i centri di gravità di tre grandezze sono su una retta e le grandezze hanno peso uguale e se anche le rette comprese fra i centri sono uguali, il centro di gravità della grandezza composta da tutte le grandezze sarà il punto che è anche il centro di gravità della grandezza di mezzo) e del relativo corollario II (Il II Corollario specifica che se nel sistema precedente viene trascurata la grandezza di mezzo, il centro di gravità del sistema sarà lo stesso di prima).
Il postulato I dal punto di vista di Archimede è intuitivo secondo un criterio di simmetria. Tuttavia da un punto di vista moderno non è del tutto evidente, in quanto occorrono esperimenti per dimostrarlo. Il Postulato VI è più problematico e meno intuitivo del Postulato I. Secondo l’interpretazione più accreditata, il Postulato VI significa che sostituendo corpi posti a determinate distanze dal fulcro ed in equilibrio con altri corpi costituiti dello stesso volume e materia, se i nuovi corpi fossero di forme diverse ma alle stesse distanze, allora l’equilibrio sarebbe mantenuto,. La Proposizione 5 afferma che tre pesi uguali i cui centri di gravità sono su una retta e sono a distanza uguale l’uno dall’altro, il centro di gravità della grandezza composta da tutte le grandezze sarà il punto centrale, che è anche il centro di gravità. Il corollario II aggiunge alla Proposizione 5 che se eliminiamo il peso sospeso nel punto centrale, il baricentro rimarrà invariato. Si giunge quindi alla Proposizione 6, che contiene il noto principio della leva.
La Proposizione 6 ha prodotto nel tempo un appassionato dibattito riguardante soprattutto l’autoevidenza dei postulati su cui si basa la Proposizione e l’assunto implicito che l’unica variabile fisicamente rilevante per descrivere l’equilibrio e la sua rottura sia il prodotto tra “P” (peso) e “L” (lunghezza del braccio). Alla base delle critiche possiamo collocare l’assenza della dimostrazione che mostri la relazione geometrica tra la posizione dei baricentro di pesi e fulcro di un sistema.
Un’importante interpretazione del principio della leva è data da Bernardino Baldi nel commento alle Questioni Meccaniche. Secondo Baldi, bracci e pesi possono essere ritenuti equipollenti. Sebbene questa equivalenza fosse nota, tuttavia non era formalmente accettata l’idea di poter porre in relazione grandezze non omogenee come peso e distanza.