Descrizione
Nelle Questioni Meccaniche, attribuite ad Aristotele, si riconducono le proprietà della leva e, in generale, dei movimenti meccanici alla natura del cerchio. Secondo l’autore, se non venisse ostacolato dal fulcro o dal piano di appoggio, il braccio della leva descriverebbe con il suo movimento una figura circolare. Per questo motivo il movimento del braccio della leva sottoposto a una forza può essere equiparato a un raggio che traccia una circonferenza. Scrive l’autore che il cerchio ha in sé la compresenza simultanea di contrari: 1) il cerchio è generato da ciò che sta fermo e da ciò che è mosso (il riferimento è alla costruzione della figura mediante compasso); 2) la linea che delimita il cerchio è caratterizzata dalla compresenza di concavo e convesso; 3) il cerchio si muove allo stesso tempo con movimenti contrari, in quanto la linea che descrive il cerchio ritorna sempre al punto da cui è partita; 4) il raggio non si muove con la stessa velocità in tutti i suoi punti, tanto che il punto più distante dal centro si muove con maggiore velocità rispetto al punto più vicino al centro. Secondo l’autore quest’ultima peculiarità è dovuta al fatto che la linea del cerchio è necessariamente generata da un duplice movimento caratterizzato da un rapporto non costante tra i due moti. Nel commento alle Questioni Meccaniche, l’urbinate Bernardino Baldi ritiene invece che 1) il cerchio non sia generato da ciò che sta fermo e dal moto, ma solo dal moto e dal fatto che il raggio durante il movimento mantiene sempre la stessa lunghezza; 2) il cerchio non sia l’unica figura che presenta una linea che è allo stesso tempo concava e convessa, ma qualsiasi linea curva presenta questa caratteristica; 3) il cerchio non sia prodotto da spostamenti contrari; 4) il cerchio non sia necessariamente generato da un moto misto (uno naturale e uno violento) e dal rapporto non costante tra i moti (causa secondo Aristotele della linea circolare), perché il moto misto potrebbe generare anche una retta (es. diagonale di un rettangolo) e da un rapporto non costante si potrebbe ottenere anche una figura diversa dal cerchio come un ellisse. Baldi conclude esaminando i giusti rapporti per disegnare figure circolari concentriche. Sempre nella stessa parte del commento, Baldi pone un’equivalenza tra i rapporti tra lunghezze di circonferenze e i rapporti tra velocità con cui i punti, che costituiscono le rispettive circonferenze, percorrono gli spazi delle dette circonferenze in una certa frazione di tempo (s = vt). L’intuizione di Baldi è interessante, in quanto introduce la relazione tra spazio, tempo e velocità nell’analisi dei movimenti meccanici [1].
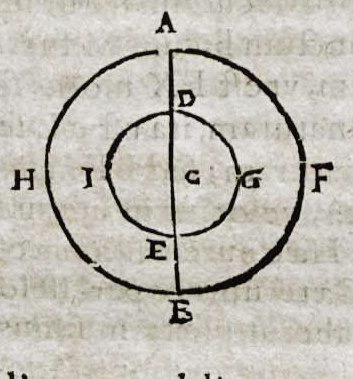
[1] «Quindi come AC sta a CD così la circonferenza AFBH sta alla circonferenza DGEI. Ma muovendo la linea CA intorno al centro C ruota pure, contemporaneamente, CD; dunque i due punti A e D compiono una rotazione nel medesimo tempo; pertanto A, percorre nello stesso tempo uno spazio maggiore, e perciò è più veloce. Allora la velocità sta alla velocità come la circonferenza alla circonferenza, come il diametro al diametro, per cui ciò che si muove in un punto più lontano dal centro, si muove più rapidamente di ciò che ne dista di meno; come dovevasi dimostrare», Baldi, 2010, p. 91 (1)